Revisiting Conference Ratings

© Copyright 2009, Paul Kislanko

In the past, I've included a conference summary in my analysis of Kenneth Massey's rating comparison data. That wasn't a conference ranking, it was just a summary of teams' ranks, and the order was based upon highest-ranked team in the conference.

For the 2009 season Dr. Massey has added conference rankings to his presentation, so I have altered my report to order conferences based upon a ranking similar to his. My order may not be exactly the same as the one on Dr. Massey's page becasue:

Note that only the order in which the conferences are listed on my report has changed. All of the data in the report is still based upon the results presented in the "Majority Consensus Summary" section of my analysis, and the team rankings on the report are not the basis of the order.

This is as good a time as any to review alternative methods of summarizing ratings at a group level. The group might be conference, or it might be the list of a team's opponents. Aside from providing ammunition for bar arguments, there are some good reasons to do this.

Averages of ranks are not always the best way to characterize conference strength (though that of Dr. Massey is better than most because of the sheer number of data points included in the average - #teams in conference × #ratings.) Often it is helpful to know something about the distribution of teams' ranks (or rating values, see below) - one really bad team in a conference can have a serious affect on the average for a conference that remains nonetheless very difficult to achieve a good conference record for the teams playing their conference schedule.

It is a little harder to create a metric that depends upon distribution when working with ranks: there's not as much difference between #40 and #60 as there is between #10 and #30. A few years ago I chose to use something I called the Weighted Median. A truly terrible name (it's really a "shifted" median), but essentially it adjusts conference ranks by how top or bottom -heavy the conference is based upon its constituent teams' ranks.

ix #Teams WtdMed Best Med Worst Conf T1 T2 T3 T4 T5 T6 T7 T8 T9 T10 T11 T12 T13
1 12 6.42 3 26 98 B12 3 4 12 17 21 26 27 60 67 72 78 98  
2 12 14.08 17 34 80 ACC 17 20 29 31 33 34 36 42 50 51 58 80  
3 10 15.5 3 30 111 P10 3 12 16 19 30 46 56 62 100 111      
4 8 19.75 25 33 94 BigE 25 27 32 33 40 47 76 94          
5 12 20.92 1 45 81 SEC 1 10 13 14 18 45 45 48 50 52 54 81  
6 1 34 47 47 47 ND 47                        
7 11 35.27 6 48 100 B10 6 7 21 36 47 48 55 65 66 69 100    
8 9 77.11 11 75 109 MW 11 11 27 60 75 81 89 96 109        
9 2 84 59 59 111 Ind 59 111                      
10 9 104 12 82 119 WAC 12 61 72 77 82 96 103 116 119        
11 12 104.92 42 86 114 CUSA 42 51 54 55 62 86 87 90 93 100 113 114  
12 13 123.23 65 93 115 MAC 65 71 73 76 79 89 93 94 100 103 106 109 115
13 9 134.56 61 97 119 SBC 61 88 92 96 97 101 107 117 119        
is an example using the September 3, 2009 Majority Consensus report to assign ranks to teams. You'll notice that for conferences with an even number of teams I don't use the arithmetical median - I choose the best rank that includes at least half the teams in the conference.

Average Values

When we have access to a rating's values (not just ordinal ranks) we can do a better job of characterizing the distribution. For example, Jeff Sagarin uses a weighted average he calls the Central Mean to discount the effects of outliers at the top and bottom of the conference team list. Graphically, his weights by team rank within conference look like this:
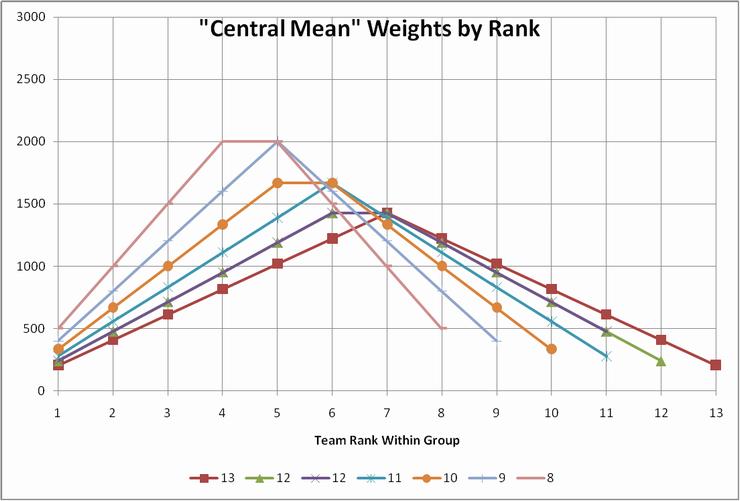Central Mean Weights x 10000
(Divide the values on the vertical axis by 100 to get percentage contributions for each rank.)

For the ratings I calculate, I'll use an even more extreme emphasis to calculate a weighted average:

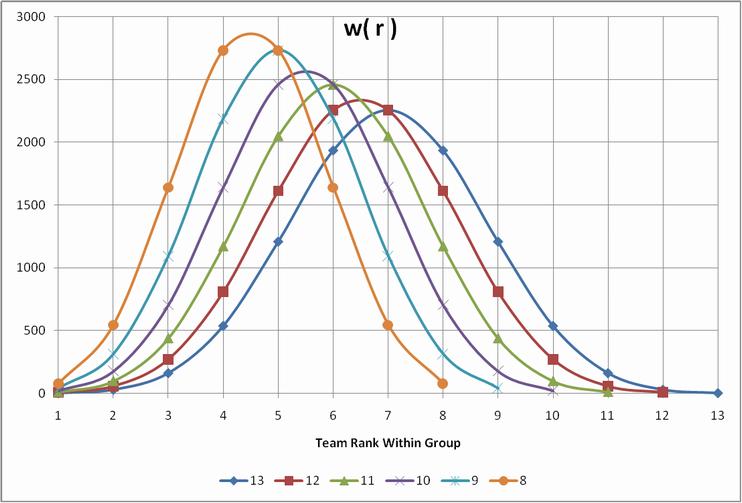
Weights by rank within conference

Comparing the two weighting systems for group size 12 shows how extreme my choice is compared to Sagarin's:

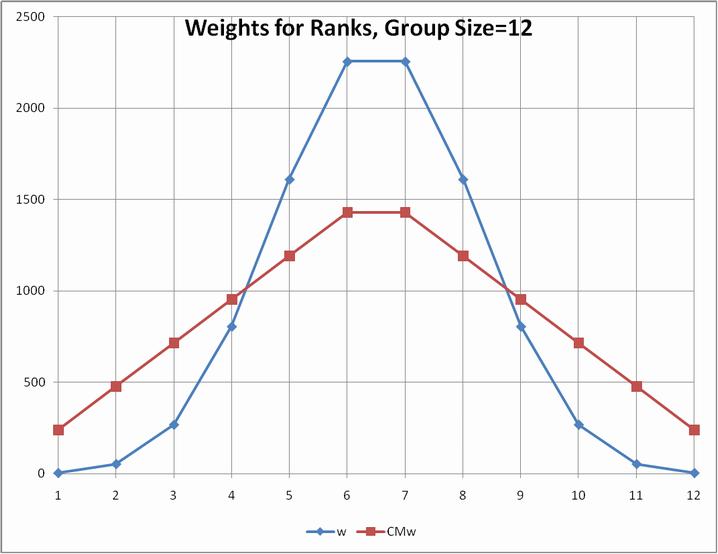12-team group weights
It may surprise you as much as it did me that the resulting weighted averages are nearly identical when applied to the Sagarin ratings (the ones I calculate will not be available until after the third weekend.)
#Teams CM WtdAvg Rank Conf T1 T2 T3 T4 T5 T6 T7 T8 T9 T10 T11 T12 T13
12 79.76 79.28 1 SEC 93.95 88.55 86.59 83.93 80.60 79.39 78.72 76.95 76.55 75.24 73.49 67.88  
10 78.30 78.38 2 P10 95.75 85.07 83.86 83.32 78.47 78.10 74.57 71.90 67.35 66.60      
12 78.25 78.33 3 B12 92.19 90.95 84.16 83.07 80.09 80.08 79.45 73.19 72.59 71.39 67.10 65.37  
12 77.64 77.62 4 ACC 85.98 82.30 81.65 81.40 78.92 77.56 76.93 76.19 76.11 73.98 73.01 65.06  
8 76.34 76.66 5 BigE 84.48 77.41 77.37 77.34 76.96 74.91 74.88 63.76          
11 75.93 75.65 6 B10 89.29 86.58 79.63 78.32 77.66 76.36 73.17 71.92 71.55 70.05 64.06    
1 75.02 75.02 7 ND 75.02                        
9 71.28 70.78 8 MW 84.18 83.49 80.81 73.40 69.82 67.39 63.31 62.46 61.23        
2 65.02 65.02 9 Ind 72.85 57.18                      
12 64.56 64.37 10 CUSA 73.69 71.21 70.69 69.87 65.00 64.83 62.96 62.92 62.73 59.56 56.04 56.03  
9 63.59 63.48 11 WAC 82.93 70.38 69.95 67.83 61.90 61.38 56.92 54.14 50.77        
13 61.23 61.05 12 MAC 67.29 65.24 65.11 64.90 63.21 61.01 60.47 60.33 60.31 58.67 58.44 56.69 55.04
9 58.88 58.88 13 SBC 70.04 62.22 60.96 59.54 59.12 58.28 56.48 53.84 50.73        
See Weigted Average definition for the derivation of the weights I will use.

What has become my favorite characterization of conference strength is based upon the fact that advanced ratings usually have values distributed normally - the "bell curve." Using Sagarin's pre-season ratings as an example (since mine aren't available until after the third weekend) we find:

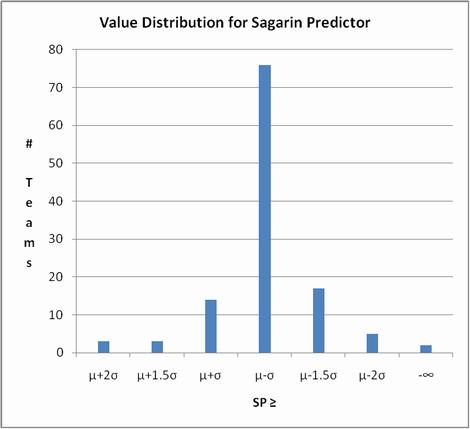Sagarin Rating value distribution
We can assign letter grades to the teams in each bucket left to right as A+ for teams' whose rating is more than 2 standard deviations above average, A for those more than 1.5 SDs above average, B for those > 1 SD above averaage, C for those whose values are within ± 1 SD of the average, and D, E, F as indicated. Then just calculate a "GPA" for each conference to use as the sort key.

In practice I divide the C bucket into C+, C and C- at average ± ½ SD. The results for the pre-season version of Sagarin's ratings:
Ix Conf A+ A B C+ C C- D E F
1 SEC 1 1 2 4 4 0 0 0 0
2 P10 1 0 3 2 4 0 0 0 0
3 B12 1 1 2 3 4 1 0 0 0
4 B10 0 1 1 3 5 1 0 0 0
5 ACC 0 0 2 5 4 1 0 0 0
6 BigE 0 0 1 4 2 1 0 0 0
7 MW 0 0 2 1 3 2 1 0 0
8 ND 0 0 0 0 1 0 0 0 0
9 WAC 0 0 1 0 3 1 2 1 1
10 Ind 0 0 0 0 1 0 1 0 0
11 CUSA 0 0 0 0 4 5 1 2 0
12 MAC 0 0 0 0 1 4 7 1 0
13 SBC 0 0 0 0 1 1 5 1 1
                   
  SP≥ μ+2σ μ+1.5σ μ+σ μ+½σ μ-½σ μ-σ μ-1.5σ μ-2σ -∞
  All: 3 3 14 22 37 17 17 5 2

For my ratings this year I'll report the weighted median summary, the weighted average, and the "GPA" report for conference characterizations.