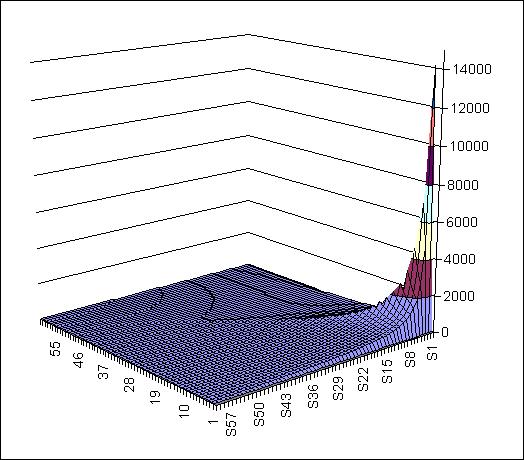
(Sn is the label for R2=n)
It occurs to me to define an objective measurement of the "interest factor" based upon the teams' ranks and their difference. If the opposing teams' ranks are R1 and R2 and N is the total number of teams (120 this year):
|
This value ranges from zero (any game involving the lowest-ranked team) to 14161 when #1 plays #1. Games between top 25 teams will have a value greater than about 230, and games between teams ranked in the top half of the field a value greater than 60.

Of course, not every combination of ranks occurs in practice. For 2007, the "interest factor" for top-60 vs top-60 games can be graphed this way:
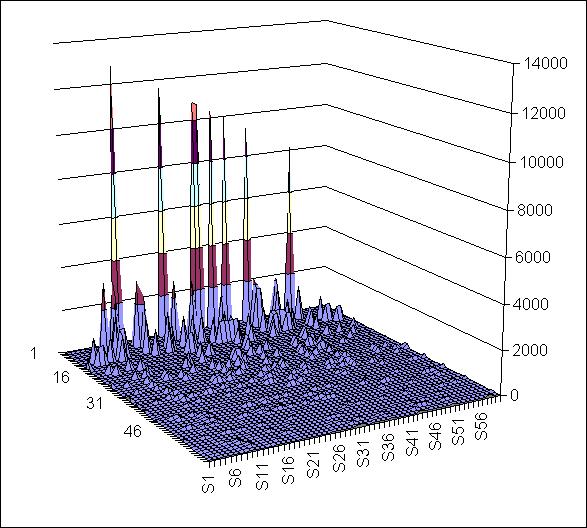
It only remains to define the ranking that's suitable for this process. The polls aren't useful, since they don't rank every team. I use Kenneth Massey's Rating Comparison (without the human polls) but not the overall ranking he defines as the average rank. Instead, I use the Majority Consensus, (see the Maj column, which is approximately the median rank.) The ranking used is the one that is the best for which 50 percent plus one of the computer rankings are as good. Hence there can be (and are) multiple teams with the same rank.
|
|
Since the formula combines ranking difference with how high the rankings are, a more interesting summary of games might be conference games for each conference. So, we rate the conference schedules by interest value of conference games as follows:
|
There's no reason to think this way of measuring conference schedules provides any more insight than any other method, but it's pretty easy to implement, and laziness, not necessity, is the mother of invention. So I'll use it this year to provide a "games of the week" list using the updated ratings.