Refining the ISR Definition

© Copyright 2010, Paul Kislanko

It has always bugged me that I have not the skill to prove the Iterative Strength Rating to be "well-defined" in the sense that all the sequences

ISR1(t1), ISR2(t1), ISR3(t1), ...
ISR1(t2), ISR2(t2), ISR3(t2), ...
ISR1(t3), ISR2(t3), ISR3(t3), ...
...
can be proven to all be convergent.

The I in ISR is for itetrative, because in shorthand

ISRn+1(team) = F(ISRn(team), ISRn(opponent 1), ISRn(opponent 2), ... ,ISRn(opponent last))[1]
In theory, ISR(t) would be defined as
(1)    LimISRn(t)
 n→∞
but for practical computational purposes we approximate that by
(2)    ISRm(t)
with m chosen so that the difference between (1) and (2) (the error) is "suitably small."

But there's a problem. We can only talk about "the error" if we know that (1) exists (for all teams.) It's easy to prove that it doesn't exist unless all teams are "connected" to each other by a chain of "A played B played C played ..." games (a necessary condition) but it is hard to prove that connectedness is sufficient for all the sequences to converge.

There is evidence that the sequences do converge[2], so the next question is what do we main by "suitably" small?

The historical definition of m is "m is the smallest n" for which:
Maxt| ISRn(t) - ISRn-1(t) |< η=0.01

This is a reasonable choice, but it does not mean that all of the values are correct to two decimal places as I've implied by my reports. (The inventor of the ISR uses this convergence criterion more correctly, reporting values only to a tenth of a unit.) The error is not large, but for the 2009 season only 68 of the 232[3] teams in the field had errors[4] less than ± .005 after the m=51 iterations it took to meet this criterion.

The reason is that even if all of the sequences converge, they do not do so at the same rate. So for 2010 and going forward, I'm using a criterion that applies to the entire system of sequences:

∑t| ISRn(t) - ISRn-1(t) |< η=0.1

For the 2009 game-set, only two teams' values are off after m=67 iterations (corresponding to the new criterion) when rounded to two decimal digits: Bethune-Cookman's value is 0.00522904 too high, and Hampton's is 0.00509839 too high.

Obviously I could just use the criterion that no team's ISR changes from iteration n to n+1 with the default precision, but there's very little to be gained from the extra 100 or so iterations that takes and it would require significantly more iterations than that until the season is complete.

The change is insignificant in terms of the rating, but it does change some rankings in the great middle range where rating values are already close. Probably no one would've noticed if I hadn't pointed it out.

Notes

 [1] The recurrence relation for the ISR is
ISRn+1(t) = 1{∑wins[ ISRn(t) + ( ISRn(opp) + ƒ(win) ) ] + ∑losses [ ISRn(t) + ( ISRn(opp) - ƒ(loss) ) ] }
#games
and ISR0(x) = 100 in the standard version, but any nonzero value will work.
ƒ(game) = k ± hfa where:
k
= 25 in the standard version, but is arbitrary.
hfa
= k/10, based upon empirical data. It is zero for neutral site games, and the sign is chosen based upon game location.

 [2] If a team has played k games then when the ISRn for a team is written as a polynomial in x,y and z (the possible values for neutral site win/loss, and non-neutral site win/loss) there's essentially a k-n term involved. Unfortunately, in order to use this fact we have to assume what was to be proved for all of the k opponents' ISRn-1.

The magnitude of the largest difference between ISRn+1(t) and ISRn(t) appears to decrease exponentially. Calculated values for iteration n correlate to AeBn (where B is negative) with an r2≈0.98 and the sum of magnitudes does with r2≈0.99. Alas, as a function of n, ∑t | ISRn(t) - ISRn-1(t) | is not monotonically decreasing, so we can't assume we can find B such that beyond some iteration the value is always < the exponential function known to converge to 0.

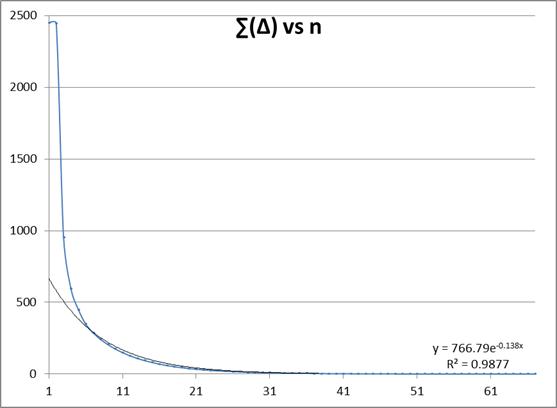
graph of SUM(Deltas) and Ae^(Bn) vs # iterations

 [3] The ISR report ranks the 120 teams in the Football Bowl Subdivision (1-A), but the game-set includes all the Football Championship Subdivision (1-AA) teams that have an FBS team either as an opponent or opponents' opponent. In 2009 there were 13 FCS teams that did not meet the criterion for inclusion.

 [4] While we don't know what (1) is (if it exists) we can compare the values we get with η=0. This is really dependent upon the precision (number of significant digits) used to calculate the values of ISRn(t), essentially setting η = 10-d for d+2 digit precision. When we use 100 significant digits and the 2009 game-set no team's values change with the 1915th iteration.

Taking the 100-digit results as the "correct" values and using 9 digit precision for all other calculations we get:
Criterion# of Iterations# within ± .005 Maximum Error
Max | ISRn(t) - ISRn-1(t) | < 0.0151680.0362
∑ | ISRn(t) - ISRn-1(t) | < 0.1672300.0052
All | ISRn(t) - ISRn-1(t) | = 0 1602322.35×10-5
All | ISRn(t) - ISRn-1(t) | < 10-981915232 Defined 0