Weighted Retrodictive Ranking Violations 2.0

© Copyright 2008, Paul Kislanko

Last year I used what I called a "surprise factor" to assign a weight to "upsets" according to the various rating systems. I never really liked the weighting I used in the Weighted Retrodictive Ranking Violation report, because the weights tended to zero too quickly. An upset of #25 only contributed .04 × ΔScore×ΔRank.

During the college baseball season I finally got around to defining an improvement, using these criteria:

• Ranking violations of top teams should count more than middle or bottom teams
• RVs above rank N should count more than one and RVs below rank N less than one
• All RVs should count at least ½.

The improved calculation is:

Surprise = ⌈ (WS - LS)÷8 ⌉ × (WR - LR) × k loge(LR2+1)

⌈ x ⌉ is the least integer ≥ x (this is the MOV expressed as # of scores) WS = Winner's Score LS = Loser's Score WR = Winner's Rank (note - in these games will be > LR) LR = Loser's Rank (that of the better-ranked team) k = loge(N2+1) where N is the desired weight=1 rank.

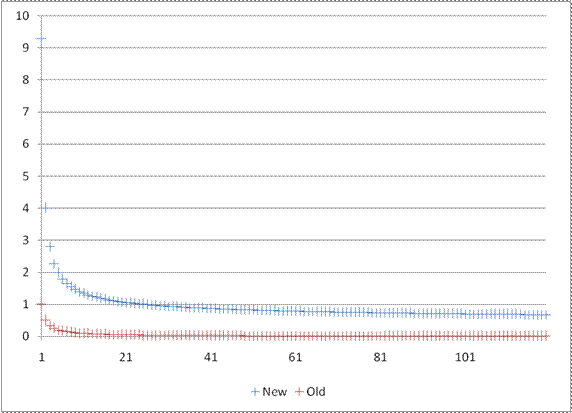
For FBS football with 120 teams, N=25 seems a logical choice, and the resulting weightings by loser's rank look like this:

• A loss by the team ranked #1 (after the loss) counts about 9.3×ΔRank×#scores-defeated-by. This drops to almost exactly 4 for a loss by #2, 2.8 for #3, 2.3 for #4 and nearly 2 for #5. A #10 loss counts about 1.4, and it decreases from there down to 1 violation per loss by #25 to a worse-rated opponent.
• 25 does seem to be an appropriate cutoff, but if we had a P-team playoff we might choose N=P.
• With 120 teams and N=25 the smallest weight for a ranking violation is a little over 2/3. If all 244 division one teams are rated the smallest violation weight is about 0.5857. As long as N ≥ ⌈ √M ⌉ (where M is the number of ranked teams) the weight will be ≥ ½.

With the new calculation, the WRRV for 2007 looks like this. Be careful with the interpretations, QPR is only "best" by this metric because it only ranks 50 teams.

Unification

Top 10 Games for 28 Aug-1 Sep

Sat Illinois @ Missouri Sat Southern Cal @ Virginia Sat Hawaii @ Florida Mon Tennessee @ UCLA Sat Utah @ Michigan Sat East Carolina vs Virginia Tech (Charlotte NC) Sat Alabama vs Clemson (Atlanta GA) Sat Washington @ Oregon Sat Florida Atlantic @ Texas Sun Kentucky @ Louisville

I like the function ƒ(R1,R2) = k ⁄ log_e(MIN(R1,R2)²+1) well enough that I will use it for more than rating rating systems. Here we just replace LR="loser's rank" with LR="Lower Rank", by which we mean "better" rank.)

To find the most interesting games, just use Game Interest = (M+1−MAX(R1,R2))׃(R1,R2) (where M is the number of ranked teams - in all of this, M+1 is the rank assigned to any unranked team.)

The coefficient (M+1)-(rank of lower-rated team) just gives a multiplier of 1 for the worst team up to 120 (for D-1A) for a game involving the #1 team. The highest value for a regular-season game in 2008 based upon 2007 rankings is 1086.9 for #4 Georgia at #1 LSU. In fact, the top 9 are all games involving LSU, but this is ok - games involving the #1 are inherently of interest. Even if the opponent's rank is really bad, the game is interesting because an upset would be a really big one.

For the first weekend, the algorithm gives these as the top 10 games.

If strikes me that if we choose N so that playing the team ranked last counts as close to ½ as we can get we can define another reasonable measure of schedule strength. The derivation of that will come in another essay.